$33,297.3
Step-by-step explanation
to know the future value of that amount we need to use the formula
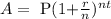
where
P is the principal ( initial amount)
r is the rate ( in decimals)
n is the number of times the interest is compounded per unit t
t is the time
so
Let
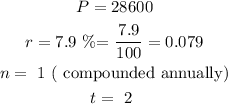
now, replace and calculate
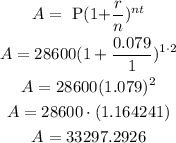
therefore, the answer is
$33,297.3
I hope this helps you