Question

If Kevin gives Diana $16, he will have the same amount of money as her. If Diana gives Kelvin $20, the amount of money she has will be 10% of his. How much money has each of them

Answer 1

Let call the amount Kevin has x and the amount Diana has y.

The equations describing this situation are

`x-16=y`
`y-20=0.1x`

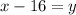
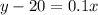
Let us now solve the system.

The first equation gives us

`x=y+16`

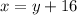
putting this into the second equation gives us

`y-20=0.1(y+16)`

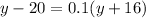
which simplifies to

`y-20=0.1y+1.6`

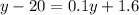
Combing terms gives us

`0.9y=21.6`

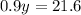
and dividing both sides by 0.9 gives us

`y=24`

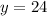
And now we solve for x.

`x=16+24`

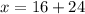
x = 40 and y =16

which is our answer!