We are given the graphs of the functions g(x) and f(x)
a) (g+f)(1)
it can be written as

From the graph, we see that the values of the two functions at x = 1 are
g(1) = -1
f(1) = 1
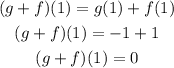
Therefore, (g+f)(1) = 0
b) (f-g)(-1)
It can be written as

From the graph, we see that the values of the two functions at x = -1 are
g(-1) = 3
f(-1) = -1
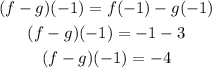
Therefore, (f-g)(-1) = -4
c) (g*f)(1)
It can be written as
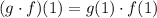
From the graph, we see that the values of the two functions at x = 1 are
g(1) = -1
f(1) = 1
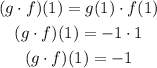
Therefore, (g*f)(1) = -1
d) (f/g)(4)
It can be written as

From the graph, we see that the values of the two functions at x = 4 are
f(4) = 0
g(4) = 0
![((f)/(g))(4)=(f(4))/(g(4))=(0)/(0)=\text{undefined}]()
Therefore, (f/g)(4) is undefined.