Question

Find the area of a dodecagon with a radius of 20 cm. round your answer to the nearest tenth.

Answer 1

The area is 1200cm²

Step-by-step explanation:

To solve this problem, we need to find the side length. We can divide the dodecagon in isosceles triangles

The angle A we can calculate it, because the dodecagon is composed by 12 triangles like this. Since the sum of all angles A add up to a whole circle:

`\angle A=(360º)/(12)=30º`

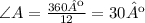
Since each triangle is an isosceles triangle, the two angles at the bottom are the same. Also, the sum of the internal angles of a triangle is 180º. Then:

`\begin{gathered} A+B+B=180º \\ 30º+2B=180º \\ B=(180º-30º)/(2) \end{gathered}`
`B=75º`

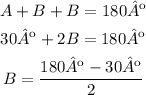
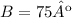
And finally, we can calculate x, which is half of the length of each side, using trigonometric relationships. In this case, we can use cosine:

`\cos(B)=(x)/(r)`

Then:

• B = 75º

,

• r = 20cm

`\begin{gathered} \cos(75º)=(x)/(20cm) \\ x\approx5.176cm \end{gathered}`

Then, the length of the side is twice x:

`L=2\cdot5.18cm=10.35cm`

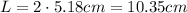
Now we can use the formula for the area of a dodecagon:

`A=3(2+√(3))\cdot L^2`

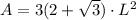
Then:

`A=3(2+√(3))(10.35)^2=1200cm^2`

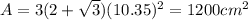
The area is 1200 squared cm.