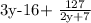Problem:
Remember :
If P(x) and D(x) are polynomials, then there exist unique polynomials Q(x) and R(x) such that:
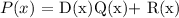
where
P(x) is the dividend
D(x) is the divisor
Q(x) is the quotient
R(x) is the remainder
Now, to solve the problem we will use the long division :
from the above, we have that
P(x) = the dividend = 6y^2 -11y+ 15
D(x) = the divisor = 2y + 7
Q(x) = the quotient = 3y-16
R(x) = the remainder = 127
then we can conclude from:
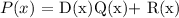
that:
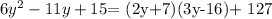
Now, Dividing the previous expression by the divisor 2y+7, we obtain:

then the correct answer is the first one: