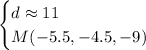Question

Identify the distance between points (-3,0,-7) and (-8,-9,-11), and identify the midpoint of the segment for which these are the endpoints. round to the nearest tenth, if necessary.

Answer 1

To find the distance and the midpoint between those points, we just need to use the distance formula and the midpoint formula. The distance formula is

`d((x_1,y_1,z_1),(x_2,y_2,z_2))=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}`

and the midpoint formula is

`M((x_1,y_1,z_1),(x_2,y_2,z_2))=((x_1+x_2)/(2),(y_1+y_2)/(2),(z_1+z_2)/(2))`

Using those formulas in our problem, for the distance we have

`\begin{gathered} d((-3_{},0,-7),(-8,-9,-11)) \\ =\sqrt[]{((-8)-(-3))^2+((-9)-(0))^2+((-11)-(-7))^2} \\ =\sqrt[]{(-8+3)^2+(-9-0)^2+(-11+7)^2} \\ =\sqrt[]{(5)^2+(-9)^2+(-4)^2} \\ =\sqrt[]{25+81+16} \\ =11.0453610172\ldots\approx11.0 \end{gathered}`

and for the Midpoint, we have

`\begin{gathered} M((-3_{},0,-7),(-8,-9,-11)) \\ =(\frac{(-3)+(-8)_{}}{2},((0)+(-9))/(2),\frac{(-7)+(-11)_{}}{2}) \\ =((-3-8)/(2),(0-9)/(2),\frac{-7-11_{}}{2}) \\ =((-11)/(2),(-9)/(2),\frac{-18_{}}{2}) \\ =(-5.5,-4.5,-9) \end{gathered}`

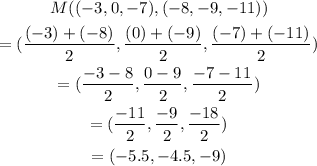
And those are our answers.

`\begin{cases}d\approx11 \\ M(-5.5,-4.5,-9)\end{cases}`