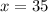Assuming that "l" and "m" are parallel, we solve this by corresponding angles.
The term corresponding angles is often used when two lines are cut by a third line, a transversal. The corresponding angles postulate states that if "l" and "m" are parallel, then the pairs of corresponding angles are congruent.
Therefore we can do the following equality:

Now, we solve to "x"

In conclusion, the answer is: