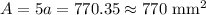Question

What is the area of the regular pentagon with a radius of 18mm?

Answer 1

Given:

Required:

We need to find the area of given pantagon

Step-by-step explanation:

First take one triangle with center angle is

`(360)/(5)=72\degree`

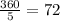
now triangle is as

use sin function to find b

`\begin{gathered} sin36=(b)/(r) \\ \\ b=10.58\text{ mm} \end{gathered}`

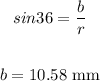
B is

`B=2b=2*10.58=21.16\text{ mm}`

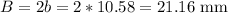
now to find h

use cos function

`\begin{gathered} cos36=(h)/(r) \\ \\ h=14.56\text{ mm} \end{gathered}`

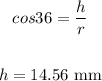
area of one triangle is

`a=(1)/(2)Bh=(1)/(2)*14.56*21.16=154.07\text{ mm}^2`

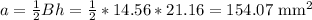
area A of pentagone is

Final answer:

`A=5a=770.35\approx770\text{ mm}^2`