Part 1
The circle is centered at the origin.
The highest point on this leg of the roller coaster is 30 feet above the ground.
• This means that the radius of the circle = 30 feet
The equation for a circle centered at the origin is:
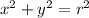
Substitute r=30 into the equation above.
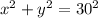
To get the equation that models the height of the roller coaster, we solve for y.
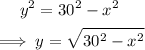
Since the roller coaster is above ground, we are only interested in the positive root.
Part 2
A graph of the model is attached below:
Model 1
If the beams are to be fastened to the rollercoaster at a height of 25 feet.
Then the height, y=25 feet.
Part 3
From the equation obtained in part (1).
![\begin{gathered} y=√(30^2-x^2) \\ \text{When y=25 feet} \\ 25=\sqrt[]{30^2-x^2} \\ Square\text{ both sides} \\ 25^2=30^2-x^2 \\ \implies x^2=30^2-25^2 \\ x=\pm√(30^2-25^2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yegcgeh8p01jk2sevvz5okh550uhe12gpj.png)
Part 4
We solve the equation for x.
![\begin{gathered} x=\pm\sqrt[]{900-625}=\pm\sqrt[]{275} \\ \implies x=+\sqrt[]{275}\text{ or }x=-\sqrt[]{275}\text{ } \\ x=16.58\; \text{or }x=-16.58 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4a3sujzcod5fh613bz3yuv0273r5gicea0.png)
Part 5
Since x=16.58 or -16.58, place the two beams 16.58 feet away from the origin (0,0), one to the right and the other to the left.
Model 2
The equations that model the concrete strut and the cable are:
![\begin{gathered} \text{Strut:}y=\sqrt[]{2x+8} \\ Cable\colon y=x-8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/kktprw8yulr3u0rp5y1gipoyt9mlj2j6ic.png)
Part 6
The graph showing the cable and the strut is attached below:
Part 7
To determine where the cable and strut intersect, equate the functions and solve simultaneously.
![\begin{gathered} \text{Strut:}y=\sqrt[]{2x+8},Cable\colon y=x-8 \\ \implies x-8=\sqrt[]{2x+8} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n39mj1oipnx8hb79rqrgpt65xfaf0kke8j.png)
Square both sides:
![\begin{gathered} (x-8)^2=(\sqrt[]{2x+8})^2 \\ (x-8)(x-8)=2x+8 \\ x^2-16x+64=2x+8 \\ x^2-16x-2x+64-8=0 \\ x^2-18x+56=0 \\ x^2-14x-4x+56=0 \\ x(x-14)-4(x-14)=0 \\ (x-14)(x-4)=0 \\ x=14\text{ or x=4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/gqykbahc8nimq8g8pywlytqt1il3lqrodt.png)
Solve for the respective values of y:
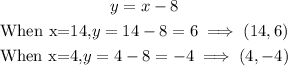
The value (4,-4) is invalid since we are dealing with heights above the ground and -4 is below the ground.
The cable and strut intersect at the point (14,6). That is 14 feet to the right of the origin and 6 feet above the ground.
Model 3
The equation of the two struts in this case are:
![y=\sqrt[]{x+8},y=\sqrt[]{x-4}](https://img.qammunity.org/2023/formulas/mathematics/college/s51obp0r5aghb3ig7igx1e0agnvriqvw7g.png)
Part 8
The graph showing the two struts is given below:
Part 9
When the two struts are two feet apart, we have that:
![\sqrt[]{x+8}-\sqrt[]{x-4}=2](https://img.qammunity.org/2023/formulas/mathematics/college/5q2hseon15w8j58k0n4up5nqno437pdcrt.png)
We solve for x.
Begin by squaring both sides.
![\begin{gathered} (\sqrt[]{x+8}-\sqrt[]{x-4})^2=2^2 \\ (\sqrt[]{x+8}-\sqrt[]{x-4})^{}(\sqrt[]{x+8}-\sqrt[]{x-4})^{}=4 \\ (\sqrt[]{x+8})^2-2(\sqrt[]{x+8})(\sqrt[]{x-4})+(\sqrt[]{x-4})^2=4 \\ x+8-2(\sqrt[]{x+8})(\sqrt[]{x-4})+x-4=4 \\ x+8+x-4-4=2(\sqrt[]{x+8})(\sqrt[]{x-4}) \\ 2x=2(\sqrt[]{x+8})(\sqrt[]{x-4}) \\ x=(\sqrt[]{x+8})(\sqrt[]{x-4}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q89b6bwn69tv3f0xpcv0h4x34ep80v2sdb.png)
Square both sides again:
![\begin{gathered} x^2=\lbrack(\sqrt[]{x+8})(\sqrt[]{x-4})\rbrack^2 \\ x^2=(x+8)(x-4) \\ x^2=x^2-4x+8x-32 \\ x^2-x^2-4x+8x-32=0 \\ 4x-32=0 \\ 4x=32 \\ x=(32)/(4)=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ehr63ea2cb66x19lqbh8lbwobhch0o0awo.png)
Part 10
At x=8, the two struts are 2 feet apart. Thus, the beam should be placed 8 feet to the right of the origin.