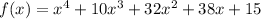Given the zeros:
• -1 with a multiplicity of 2
,
• -3
,
• -5
Let's find the equation of the polynomial.
Using the given zeros, we have the following:
x = -1, x = -1, x = -3, x = -5
Now, rewrite each zero as a factor:
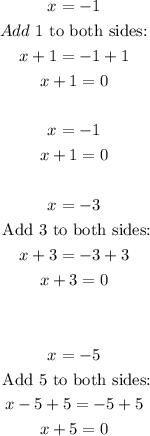
Now, we have the equation:
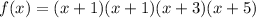
Let's expand the equation usng the FOIL method and distributive property:

Solving further:
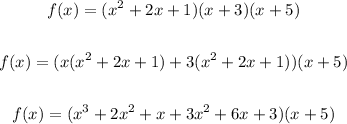
Combine like terms:

Now, apply FOIL method and distributive property once more:

Therefore, the equation of a polynomial with the given zeros is:

• ANSWER: C