The density of the gasoline used on your trip is 0.755 g/ml. What is the total mass in grams, andin ounces, of the gasoline used on your trip?15.3 L was used.

Question

asked Oct 27, 2023 204k views

1 Answer

Lieutenant Dan · Answer 1 · 2023-11-02T00:34:52+0000

Since 15.3 L was used, we can convert this to mass using the density:

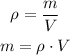
$\begin{gathered} \rho=(m)/(V) \\ m=\rho\cdot V \end{gathered}$

Using the density of 0.755 g/mL, we need to convert the volume to mL, so:

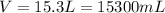
Now, using the volume and the density, we have:

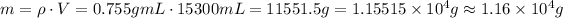
$m=\rho\cdot V=0.755g\/mL\cdot15300mL=11551.5g=1.15515*10^4g\approx1.16*10^4g$

So, the mass in grams is approximately 1.16 x 10⁴ g.

To convert to ounces, we can divide the value in grams by approximately 28.349523:

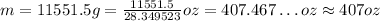
$m=11551.5g=(11551.5)/(28.349523)oz=407.467\ldots oz\approx407oz$

So, the mass in ounces is approximately 407 oz.