Given:
The set of side lengths are:
2, 3, 13
5, 7, 12
10, 24, 29,
11, 60, 61
Required:
Find the set that is a Pythagorean triple.
Step-by-step explanation:
The Pythagoras theorem is given as:
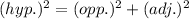
The hypotenuse side is the longest side.
Take the set 2,3,13
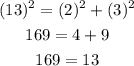
This is not true.
Take the sets 5, 7, 12
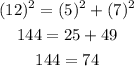
This is not true.
Take the sets 10, 24, 29
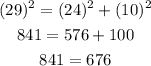
This is not true.
Take the sets 11, 60, 61
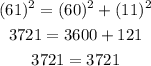
This is true.
So the set 11, 60, and 61 makes a Pythagorean triple.
Final Answer:
The last option is the correct answer.