Question

What is the graph of Y=F(X-2)+4

Answer 1

Given a function f(x), we know that the graph of:

• f(x - a) is the graph f(x) shifted horizontally ,a, units to the right,

,

• f(x) + b is the graph f(x) shifted vertically ,b, units up,

,

• f(x - a) + b is the graph f(x) shifted horizontally ,a, units to the right and vertically ,b, units up,.

Comparing the function:

`y=f(x-2)+4`

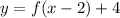
with the general case f(x - a) + b, we see that we have:

• a = 2,

,

• b = 4.

So we conclude that the graph of this function is the graph of f(x) sifted:

• horizontally a = 2 units to the right,

,

• vertically b = 4 units up.

Answer

The graph of this function is the graph of f(x) sifted:

• horizontally 2 units to the right,

,

• vertically 4 units up.