Question

6 3/5 - 2 1/4 simplify and write as a mixed number

Answer 1

Mixed numbers

A mixed number is a way to write a fractional number that is greater than 1. Mixed numbers have two parts: an integer and a fraction smaller than 1. If the integer is a and the fraction is b/c then the mixed number can be written as a fraction following this procedure:

`a\text{ }(b)/(c)=a+(b)/(c)=(ac+b)/(c)`

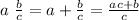
Simplifying

We must simplify this expression:

`6\text{ }(3)/(5)-2\text{ }(1)/(4)`

We can write both numbers as fractions using the formula above:

`\begin{gathered} 6\text{ }(3)/(5)-2\text{ }(1)/(4)=(6+(3)/(5))-(2+(1)/(4))=(6\cdot5+3)/(5)-(2\cdot4+1)/(4) \\ 6\text{ }(3)/(5)-2\text{ }(1)/(4)=(6\cdot5+3)/(5)-(2\cdot4+1)/(4)=(33)/(5)-(9)/(4) \end{gathered}`

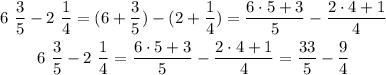
In order to perform the last substraction we can multiply and divide each fraction by the denominator of the other:

`(33)/(5)\cdot(4)/(4)-(9)/(4)\cdot(5)/(5)=(132)/(20)-(45)/(20)=(132-45)/(20)=(87)/(20)`

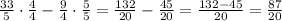
Now we have to write 87/20 as a mixed number. We can rewrite the numerator like this:

`(87)/(20)=(7+80)/(20)=(7+4\cdot20)/(20)`

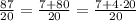
Then we distribute the division:

`(7+4\cdot20)/(20)=(7)/(20)+(4\cdot20)/(20)=(7)/(20)+4=4\text{ }(7)/(20)`

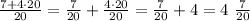
Then the answer is 4 7/20.