The sequence given:
7, 13, 19, ...
This is an arithmetic sequence.
The first term (a1) is 7.
The common difference (d) between the terms is 13 - 7 =6, or 19 - 13 = 6.
To find the 32nd term of this sequence, we are going to use the nth term formula of an arithmetic sequence, shown below:

Where
a_n is the nth term
a_1 is the first term
n is the number of the term
d is the common difference
Given,
a_1 = 7
d = 6
Let us find the 32nd term:
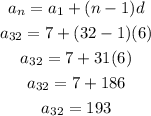
Thus, the 32nd term of this arithmetic sequence is 193.
Answer
193