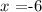Solution:
A general form o quadratic function is given by the following expression:

The vertex form of this quadratic function is given by the following expression:

where (h,k) is the vertex of the quadratic function.
PART A:
To find the vertex form of the given function, we must complete the square of this function:
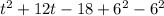
this is equivalent to:

that is:

so that, the vertex form of the given function is:
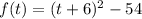
Part B: According to the previous part, we can conclude that the vertex is:
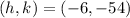
Part C: The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola. So that, we can conclude that the axis of symmetry for f(t) is: