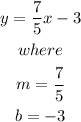Question

Points R S and T make the triangle (triangle)RST and are at the coordinates R(-43,-4), S(0,-3), and T(13,-44) Point Q is the midpoint of RT and QS is a median of RST what is the equation of the line QS? The equation of the line can be given in slope intercept form by the formula y=mx+bwhere m=____b=____

Answer 1

Explanation:

Step 1. We are given the coordinates of the three endpoints of a triangle

R(-43,-4), S(0,-3), and T(13,-44)

Which are shown in the following diagram (not to scale):

Step 2. The problem states that Q is the midpoint of the line that goes from R to T (RT):

And we need to find the equation of the line QS, shown here in yellow:

Step 3. To find the equation of the line, first, we need to find the coordinates of Q. Since Q is the midpoint between R and T, we find its coordinates by averaging the coordinates of R and T:

Step 4. Then, once we know the coordinates of point Q, we need to find the slope between Q and S. To make it easier to find the slope, we will label the coordinates of S and Q as follows:

And use the slope formula:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \downarrow \\ m=(-24-(-3))/(-15-0) \\ \downarrow \end{gathered}`
`\begin{gathered} m=(-24+3)/(-15) \\ \downarrow \\ m=(-21)/(-15) \\ \downarrow \\ m=(7)/(5) \end{gathered}`

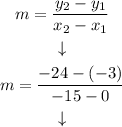
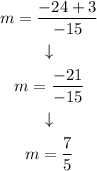
The slope is m=7/5

Step 5. The final step is to use the point-slope formula using point S as (x1,y1) and the previously found slope m

`\begin{gathered} point\text{ - slope formula:} \\ y-y_1=m(x-x_1) \end{gathered}`

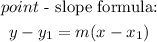
Substituting the known values:

`y-(-3)=(7)/(5)(x-0)`

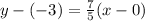
Solving the operations and solving for y:

`\begin{gathered} y+3=(7)/(5)x \\ \downarrow \\ y=(7)/(5)x-3 \end{gathered}`

Where the slope is m=7/5, and the y-intercept 'b' is b=-3.

Answer:

`\begin{gathered} y=(7)/(5)x-3 \\ where \\ m=(7)/(5) \\ b=-3 \end{gathered}`