ANSWERS
(a) 5.04 m/s²
(b) 294.34 N
Step-by-step explanation
Given:
• The mass of the planet, M = 6.14 x 10²³ kg
,
• The radius of the planet, R = 2.85 x 10⁶ m
,
• The mass of a person standing on this planet, m = 58.4 kg
(a) The acceleration due to gravity in a planet of mass M and radius R is,
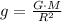
Where G is the gravitational constant with a value of 6.67 x 10⁻¹¹ Nm²/kg².
Replacing the known values and solving we get the acceleration due to gravity of this planet,
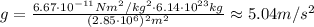
Hence, the acceleration due to gravity is 5.04 m/s², rounded to two decimal places.
(b) The weight of an object of mass m is the product of its mass and the acceleration due to gravity,
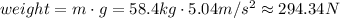
Hence, a 58.4-kg person would weigh 294.34 N on this planet, rounded to two decimal places.