Given the system of equations;

To plot each of these lines on a graph, we would need to get some points such that we could use it to draw a straight line.
For equation 1;
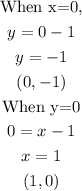
Now, you draw a line joining these points together, we have;
Similarly, we would apply same to equation 2, we have;
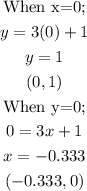
Then, we have its graph as;
Now, the combination of the two graphs is;
The solution of the system of equation is;
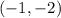
CORRECT OPTION: C