Question

Multiple-choice questions each have 6 possible answers, one of which is correct. Assume that you guess the answers to 4 such questions.Use the multiplication rule to find the probability that the first three guesses are wrong and the fourth is correct. That is, find P(WWWC)P(WWWC) , where C denotes a correct answer and W denotes a wrong answer.

Answer 1

There are 6 possible answers in a Multiple choice question out of which only one is correct. So probability for a correct answer is,

`P(C)=(1)/(6)`

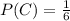
The probability for the wrong answer is,

`\begin{gathered} P(W)=1-(1)/(6) \\ =(5)/(6) \end{gathered}`

The probability for first three question wrong and fourth one is correct is,

`\begin{gathered} P(WWWC)=P(W)\cdot P(W)\cdot P(W)\cdot P(C) \\ =(5)/(6)\cdot(5)/(6)\cdot(5)/(6)\cdot(1)/(6) \\ =(125)/(1296) \\ =0.09645 \\ \approx0.0965 \end{gathered}`

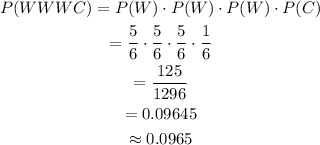
So answer is 0.0965.