Question

Hi, can you help me answer this question, please, thank you:)

Answer 1

From the question given

Past studies have shown that only about 84% of the booked passengers show up

This can be taken as the probability of success (P)

Since we are told to find the probability that if Air-USA books 21 people, not enough people will show up

Then

In this case

`\begin{gathered} P=84\text{\%=}(84)/(100)=0.84 \\ n=21 \end{gathered}`

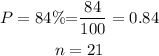
We will use the formula below to find the probability that if Air-USA books 21 people, not enough people will show up

`P(x>20)=P^n`

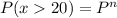
since we have the values of P and n

`P(x>20)=0.84^(21)=0.0257`

`\begin{gathered} \text{Hence,} \\ P(x>20)=0.0257 \end{gathered}`

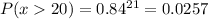
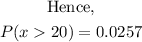
For the B part of the question

let us convert the answer obtained to percentage so we can compare it with 5% probability

`0.0257=2.57\text{ \%}`

Thus,

yes, the probability is low enough so that overbooking is low enough to be a concern.

For the part C of the question

since we have already converted to a percentage, then we will compare to 10%

Since

`\begin{gathered} 2.57\text{ \% is less than 10\%} \\ \text{Then} \end{gathered}`

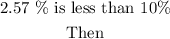
yes, the probability is low enough so that overbooking is low enough to be a concern.