Question

Which of the following vectors has a magnitude of square root of 65 and a direction of θ = 240.255°?

Answer 1

Option D u = <-4, -7>

Explanation:

The magnitude matches
`√(65)` since

`||u|| = √((-4)^2+(-7)^2)\\||u|| = √((16)+(49))\\||u|| = √(65)\\`

The direction also matches since

`tan^(-1) ((-7)/(-4)) = 60.255 \\`

Since <-4, -7> lies in quadrant three we will add 180 degrees to the reference angle.

60.255 + 180 = 240.255

Therefore, the answer is option D

Answer 2

`D)u=\mleft<-4,-7\mright>_{}`

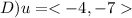
1) We can find the magnitude of a vector(a.k.a. the norm) of a vector and the direction, by making use of the following formulas:

`\begin{gathered} \mleft\|v\mright\|=\sqrt[]{a^2+b^2} \\ \tan (\theta)=(b)/(a) \end{gathered}`

2) In this question, the magnitude and the direction of that vector have been given to us. So, let's do the other way around to identify which one has this magnitude and direction.

`\begin{gathered} \mleft\|u\mright\|=\sqrt[]{(-4)^2+(-7)^2}=\sqrt[]{16+49}=\sqrt[]{65} \\ \tan (\theta)=(-4)/(-7) \\ (\theta)=\tan ^(-1)((-4)/(-7)) \\ D=\tan ^(-1)((-4)/(-7))-180 \\ D=-119.74+360 \\ D=240.2 \end{gathered}`

Note that since we want a positive value, we need to add 360 degrees.