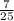Solution
- To find the equation of the tangent, we should:
1. Find the derivative of the equation with respect to x. This give us the expression for all the possible slopes of the curve.
2. Substitute the values of (x, y) = (2, 3) into the expression in step 1. This gives the particular slope of the tangent line.
3. After this, you use the formula below to find the equation of the tangent line:

- Thus, we can solve the question as follows:
STEP 1:

- Now that we have our equation for the slope, let us find the particula slope
STEP 2:
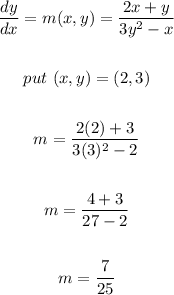
- Now that we have the slope of the tangent line, we can thus find the equation of the tangent line.
Final Answer
The slope of the tangent line is