Question

I need help solving the following equation for all values of x

Answer 1

Given the equation below

`(x+1)/(x-3)-(1)/(x+4)=(28)/(x^2+x-12)`

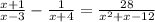
To find the value(s) of x, we find the factors of the denominators

`\begin{gathered} (x+1)/(x-3)-(1)/(x+4)=(28)/(x^2+x-12) \\ \text{Where} \\ x^2+x-12=x^2+4x-3x-12 \\ =x(x+4)-3(x+4)=(x-3)(x+4) \\ x^2+x-12=(x-3)(x+4) \\ \text{Substitute (x-3)(x+4) for x}^2+x-12 \\ (x+1)/(x-3)-(1)/(x+4)=(28)/((x-3)(x+4)) \end{gathered}`

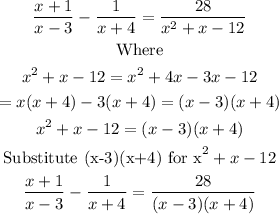
Since they have a common denominator i.e both the right and left handside, we solve for x by eliminating the denominators

`\begin{gathered} (x+1)/(x-3)-(1)/(x+4)=(28)/((x-3)(x+4)) \\ ((x+1)(x+4)-(x-3))/((x-3)(x+4))=(28)/((x-3)(x+4)) \\ \text{Eliminate the deominators} \\ (x+1)(x+4)-(x-3)=28_{} \end{gathered}`

Expand the brackets

`\begin{gathered} (x+1)(x+4)-(x-3)=28_{} \\ x(x+4)+1(x+4)-x+3=28 \\ x^2+4x+x+4-x+3=28 \\ \text{Collect like terms} \\ x^2+4x+x-x+4+3-28=0 \\ x^2+4x-21=0 \\ x^2+7x-3x-21=0 \\ \text{Factorize the equation} \\ x(x+7)-3(x+7)=0 \\ (x-3)(x+7)=0 \\ x-3=0 \\ x=3 \\ x+7=0 \\ x=-7 \\ x=3\text{ or -7} \end{gathered}`

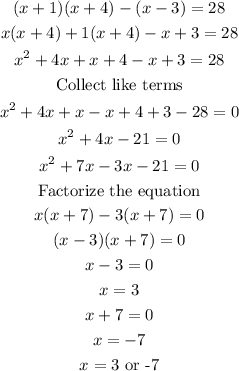
Given that the values of x are 3 or -7

To find which of the solution satisfies the given equation,

Find the undefined points of the equation, i.e

`\begin{gathered} (x-3)(x+4)=0 \\ x=3\text{ or -4} \end{gathered}`

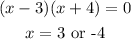
Since the equation is undefined for x = 3,

Hence, the answer is x = -7