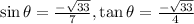Question

If cos O 4/7 and csc O<0 , find sin Oand tan O

Answer 1

Step-by-step explanation:

If cosθ = 4/7, we can represent it with the following triangle

To find the sinθ, we need to calculate the missing side x. Using the Pythagorean theorem, we get that the value of x is

`\begin{gathered} x=√(7^2-4^2) \\ x=√(49-16) \\ x=√(33) \end{gathered}`

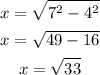
Then, sinθ and cscθ have the same sign, so sinθ will be negative and is equal to

`\begin{gathered} \sin\theta=(Opposite)/(Hypotenuse) \\ \\ \sin\theta=(x)/(7) \\ \\ \sin\theta=-(√(33))/(7) \end{gathered}`

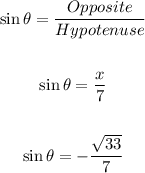
Finally, tanθ is equal to

`\begin{gathered} \tan\theta=(Opposite)/(Adjacent) \\ \\ \tan\theta=(-√(33))/(4) \end{gathered}`

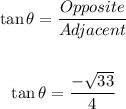
Answer:

Therefore, the answer is

`\sin\theta=(-√(33))/(7),\tan\theta=(-√(33))/(4)`