We have the expression:

In orde to determine it's relative maximum and minimum, we operate as follows:
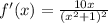
When we equal x to 0, we will have the point (0, -5).
And replacing values near 0, we will have that before 0 decreases and after 0 increases, from this, we have that the point (0, -5) is a relative minimum.