We need o find the cut-off score for acceptance.
We know that the scores are normally distributed with a mean of 500 and a standard deviation of 100.
Thus, we can use a z-score table to find Z for which the percentage above it is 25% = 0.25.
Then, we calculate the cut-off score x as follows:
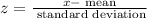
Using a z-score table, we find the the z with a percentage above 0.25 (one minus the percentage below 0.75) is:
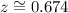
Then, we obtain:
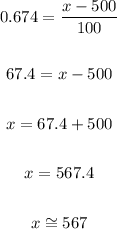
Answer: c) 567