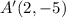Question

Find the image of point A (6, -12) using the rule(x, y) – > (x – 4, y + 7)O A' (3,0)O A' (2,-5)O A' (-4,7)0 A (-2,5)

Answer 1

The original point is:

`A(6,-12)`

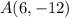
The first step will be to identify the x and y values:

`\begin{gathered} x=6 \\ y=-12 \end{gathered}`

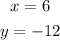
And the second step will be to apply the given rule.

The rule for the transformation is:

`(x,y)\longrightarrow(x-4,y+7)`

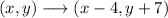
This tells us that to find the image point we have to subtract 4 to the x value and add 7 to the y value.

We apply the rule to the original point:

`(6,-12)\longrightarrow(6-4,-12+7)`

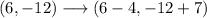
And solving the operations:

`(6,-12)\longrightarrow(2,-5)`

We have found the image point:

`A^(\prime)(2,-5)`

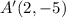
Answer:

`A^(\prime)(2,-5)`