Given
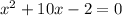
You have to determine both possible values of x by using the quadratic formula, which is:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Where
a is the coefficient that multiplies the quadratic term of the quadratic expression
b is the coefficient of the x term
c is the constant
For the given expression, the values of the coefficients are:
a=1
b=10
c=-2
Replace said coefficients in the formula and solve
![\begin{gathered} x=\frac{-10\pm\sqrt[]{10^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ x=\frac{-10\pm\sqrt[]{100+8}}{2} \\ x=\frac{-10\pm\sqrt[]{108}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/70vow4pmpcgg8zibxwwxpgwfxw2009pnz7.png)
Now you have to solve the addition and subtraction separately
Addition
![\begin{gathered} x=\frac{-10+\sqrt[]{108}}{2} \\ x=0.196 \\ x\approx0.2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ykwlc3fil5boso0scb3xm5i9b1pmn8nlkh.png)
Subtraction
![\begin{gathered} x=\frac{-10-\sqrt[]{108}}{2} \\ x=-10.196 \\ x\approx-10.20 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ogoxin2473h3ae0bfth84sze9j0lnznl60.png)
The possible values of x are -10.20 and 0.20.