We have
mr=mass rifle
mb=mass bullet
vb0=initial velocity of the bullet
vr0=initial velocity of the rifle
vbf=final velocity of the bullet
vrf=final velocity of the rifle
mr=2.68 kg
mb=69.5 g =0.0695 kg
vb0=0 m/s
vr0=0m/s
vbf=612 m/s
vrf=?
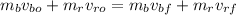
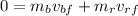
we isolate the vr
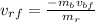
Then we substitute
![v_(rf)=\frac{-(0.0695\operatorname{kg})(612)}{2.68}=-15.871\text{ m/s}]()
The recoil velocity is -15.871 m/s