Question

The table below shows how V, the volume of a prism with a square base, changes as s, the side length of the square base, changes, andthe height of the prism remains the same.Square Prism Measurementss, Side LengthV, Volumeof Square Base2 meters16 meters3 meters 36 meters4 meters 64 meters5 meters100 metersWhich equation best represents the relationship between s, the side length of the square base of a prism, and V, the volume of a squareprism whose height remains the same?OA. V = 8sOB. V = 2(452)OC. V = 452D. V = 4(2s)

Answer 1

Write out the volume of a prism

Formula

`\begin{gathered} \text{Volume of a prism = square based area x height} \\ V=\text{ Bh} \\ \text{where B = Square based represents side length} \\ Height\text{ = h remain the same } \\ \end{gathered}`

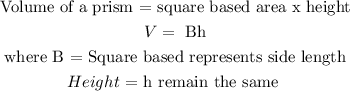
Using the first side based length and volume to derive the equation

`\begin{gathered} V=Bh=l^2h \\ V_1=16,s_1=2\text{ } \\ 2^2h\text{ = 16} \\ 4h\text{ = 16} \\ h\text{ = }(16)/(4) \\ h\text{ = 4} \end{gathered}`

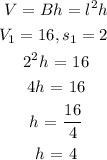
Using the third side based length and volume to derive the equation

`\begin{gathered} V=Bh=l^2h \\ V_3=64,s_3\text{ = 4} \\ 4^2h\text{ = 64} \\ 16h\text{ = 64} \\ h\text{ = }(64)/(16) \\ h\text{ = 4} \end{gathered}`

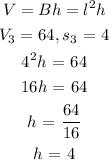
Therefore from the two result above, the equation can be deduced as

`\begin{gathered} V=4s^2 \\ \sin ce\text{ height of the prism remain the same for all the table above } \end{gathered}`

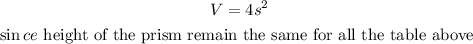
Hence the equation that best represents the relationship is V = 4s²