Question

How do we do this one it has two parts

Answer 1

Given

Average Fahrenheit temperature in a certain city during a typical 365- day year

`y=32\sin[(2\pi)/(365)(x-96)]+21`

Find

On what day the temperature is increasing fastest

Step-by-step explanation

for maximising y

`(dy)/(dx)=0`

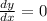
so , now we find the first derivative

`\begin{gathered} y=32\sin[(2\pi)/(365)(x-96)]+21 \\ \\ (dy)/(dx)=32\cos[(2\pi)/(365)(x-96)]*(2\pi)/(365) \end{gathered}`

put dy/dx = 0

`\begin{gathered} (dy)/(dx)=0 \\ \\ 32\cos[(2\pi)/(365)(x-96)]*(2\pi)/(365)=0 \\ \\ \cos[(2\pi)/(365)(x-96)]=0 \\ \\ since\text{ the function is maximum when }\theta=0 \\ so\text{ , }(dy)/(dx)\text{ is maximum , when } \\ [(2\pi)/(365)(x-96)]=0 \\ \\ x-96=0 \\ x=96 \end{gathered}`

so , at 96 day temperature is increasing the fastest

b) rate of change of temperature per day ,

`(dy)/(dx)=32\cos[(2\pi)/(365)(x-96)]*(2\pi)/(365)`

put x = 96

`\begin{gathered} (dy)/(dx)=32\cos[(2\pi)/(365)(x-96)]*(2\pi)/(365) \\ \\ (dy)/(dx)=32\cos[(2\pi)/(365)(96-96)]*(2\pi)/(365) \\ \\ (dy)/(dx)=32\cos0*(2\pi)/(365) \\ \\ (dy)/(dx)=32*(2\pi)/(365) \\ \\ (dy)/(dx)=0.55085460227\approx0.55 \end{gathered}`