Question

A company introduces a new product for which the number of units sold S is given by the equation below, where t is the time in months.

Answer 1

Given the equation:

`S(t)=20(7-(7)/(2+t))`

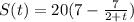
Where t is the time in months.

Let's solve for the following:

• (a). Average rate of change of S(t) during the first year.

During the first year, the time interval, t is from 0 to 12 months.

Now, to find the average rate of change for the first year, apply the formula:

`S(t)_(avg)=(S(12)-S(0))/(12-0)`

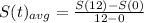
Now, let's solve for S(12) and S(0):

`\begin{gathered} S(12)=20(7-(7)/(2+12))\Longrightarrow20(7-(7)/(14))\Longrightarrow20(7-0.5)=130 \\ \\ S(0)=20(7-(7)/(2+0))=\Rightarrow20(7-(7)/(2))\Longrightarrow20(7-3.5)=70 \end{gathered}`

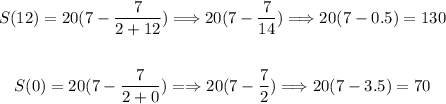
Hence, to find the average rate of change, we have:

`\begin{gathered} S(t)_{\text{avg}}=(S(12)-S(0))/(12-0) \\ \\ S(t)_{\text{avg}}=(130-70)/(12-0) \\ \\ S(t)_{\text{avg}}=(60)/(12) \\ \\ S(t)_{\text{avg}}=5 \end{gathered}`

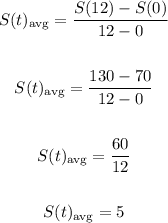
Therefore, the average rate of change during the first year is 5

• (b). During what month of the first year does S (1) equal the average rate of change?

Let's first find the derivative of S(t):

`\begin{gathered} S^(\prime)(t)=20(0+(7)/((2+t)^2)) \\ \\ S^(\prime)(t)=20((7)/((2+t)^2)) \\ \\ S^(\prime)(t)=(140)/((2+t)^2) \end{gathered}`

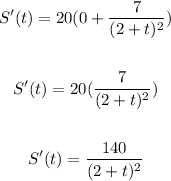
Now, we have:

`\begin{gathered} S^(\prime)(t)=S_(avg) \\ \\ 5=(140)/((2+t)^2) \\ \\ 5(2+t)^2=140 \\ \\ (2+t)^2=(140)/(5) \\ \\ (2+t)^2=28 \end{gathered}`

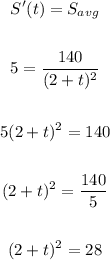
Take the square root of both sides:

`\begin{gathered} \sqrt[]{(2+t)^2}=\sqrt[]{28} \\ \\ 2+t=5.3 \\ \\ t=5.3-2 \\ \\ t=3.3\approx4 \end{gathered}`

Therefore, the month will be the 4th month which is April.

ANSWER:

(a). 5

(b). April