A sphere and a cylinder each have the same radius. The cylinder has a height that is triple the radius. How do I create a simplified expression to show how many times greater th…

Question

asked Jul 16, 2023 43.8k views

1 Answer

Mark Robbins · Answer 1 · 2023-07-20T23:48:37+0000

we are given a sphere and a cylinder with the following conditions:

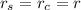
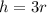
The volume of the sphere is given by the following formula:

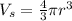
$V_s=(4)/(3)\pi r^3$

The volume of the cylinder is given by:

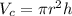
$V_c=\pi r^2h$

Since the height "h" is three times the radius "r", we get_

$V_c=3\pi r^3$

Now we divide both sides by 3:

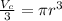
$(V_c)/(3)=\pi r^3$

Now we replace the right sides of the volume of the sphere for its equivalent in the volume of the cylinder:

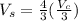
Solving:

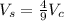
Multiplying by 9/4:

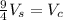
Therefore, the cylinder occupies 9/4 of the volume of the sphere.