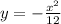Question

Using the distance formula, write an equation of the parabola given focus (0,-3) and directrix y=3

Answer 1

Recalling the definition of a parabola:

Parabola: A parabola is a curve where any point is at an equal distance from

1) a fixed point (f₁,f₂) (the focus ), and

2) fixed straight line Ax+By+C=0 (the directrix).

Therefore, a point (x₀,y₀) is on the parabola iff:

`\sqrt[]{(x_0-f_1)^2+(y_0_{}-f_2)^2}=|\frac{Ax_0+By_0+C}{\sqrt[]{A^2+B^2}}|`

Now, if the directrix is y=3 and the focus is (0,-3), then (x₀,y₀) is on the parabola iff:

`\sqrt[]{(x_0-0)^2+(y_0-(-3))^2}=|y_0-3|`

Raising the equation to power 2 and solving for y₀ we get:

`\begin{gathered} x^2_{0^{}}+(y_0+3)^2=(y_0-3)^2 \\ x^2_0+y^2_0+6y_0+9=y^2_0-6y_0+9 \\ x^2_0=-12y_0 \\ y_0=-(x^2_0)/(12) \end{gathered}`

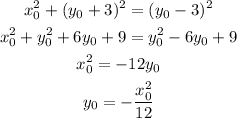
Therefore the equation of the parabola with focus (0,-3) and directrix y=3 is:

`y=-(x^2)/(12)`