Question

Need more explanation to this review/exercise so I can understand what I’m going to do in my test.

Answer 1

Given a figure of triangle ABC, whose side BC is 12 and angle A and angle B are 60 degrees.

We have to find the area of a triangle.

The area of the triangle ABC is:

`A=(1)/(2)* CD* AB`

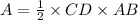
Here, we'll use the trigonometric function sine to find the length of the side CD.

In triangle BDC,

`\begin{gathered} \sin 60=(CD)/(BC) \\ \frac{\sqrt[]{3}}{2}=(CD)/(12) \\ CD=\frac{12\sqrt[]{3}}{2} \\ CD=6\sqrt[]{3} \end{gathered}`

Since two angles of the triangle are given 60 degrees. So, the triangle ABC is an equilateral triangle. Therefore, AB = BC = 12.

Now, the area will be:

`\begin{gathered} A=(1)/(2)*6\sqrt[]{3}*12 \\ =36\sqrt[]{3} \end{gathered}`

Thus, option 3 is correct.