Question

Find a degree 4 polynomial having zeros -5, -2, 4 and 8 and the coefficient of 24 equal 1.The polynomial is

Answer 1

`x^4-5x^3-42x^2+104x+320=0`

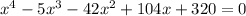
1) We are going to start with the factored form of a function. Given by this formula for a 4th-degree function:

`y=a(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

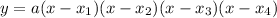
In this question, the leading coefficient has been given to us already, so we can plug into that a=1

`y=1(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

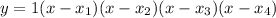
2) Now let's plug into them the other roots:

`y=(x+5_{})(x+2_{})(x-4_{})(x-8_{})`

2.2) Let's rewrite that function as an equation plugging y=0, and expanding it:

`\begin{gathered} (x+5_{})(x+2_{})(x-4_{})(x-8_{})=0 \\ x^4-5x^3-42x^2+104x+320=0 \end{gathered}`

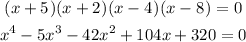
And that is the answer