Question

Which of the following is equivalent to x^2-100/2x+20 for all values of x, where x not equal to -10

Answer 1

The given expression is:

`(x^2-100)/(2x+20)`

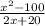
To simply the expression above, we are going to apply the difference of two squares rule for the numerator and we find the common factor for the denominator.

Thus, we have:

`\begin{gathered} (x^2-100)/(2x+20) \\ \Rightarrow((x-10)(x+10))/(2(x+10)) \end{gathered}`

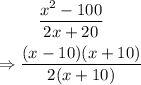
(x+10) is common to both the numerator and the denominator and as such, they will cancel out each other.

Thus, we have:

`\begin{gathered} ((x-10)(x+10))/(2(x+10)) \\ \Rightarrow(x-10)/(2) \end{gathered}`

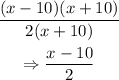
Hence, the correct option is option A