Question

There were 80 more men than women at a party. After 60% of the men and 35% of the women left the party, there were 13 more women than men. How many women were there at first?

Answer 1

Let M be the initial amount of men at the party, and W the initial amount of women.

Since there were 80 more men than women, then:

`M=W+80`

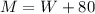
If 60% of men leave the party, then 40% remain. If 35% of women leave the party, then 65% remain.

Then, (40/100)M and (65/100)W remain at the party, Now, there are 13 more women than men. Then:

`(65)/(100)W=(40)/(100)M+13`

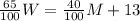
We got a 2x2 system of equations:

`\begin{gathered} M=W+80 \\ (65)/(100)W=(40)/(100)M+13 \end{gathered}`

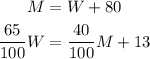
Solve the system using the substitution method. Since M is isolated in the first equation, replace M for W+80 into the second equation and solve for W:

`\begin{gathered} \Rightarrow(65)/(100)W=(40)/(100)(W+80)+13 \\ \\ \text{ Multiply both members by 100} \\ \Rightarrow65W=40(W+80)+1300 \\ \\ \text{ Expand the product on the right member} \\ \Rightarrow65W=40W+3200+1300 \\ \\ \text{ Simplify the right member} \\ \Rightarrow65W=40W+4500 \\ \\ \text{ Subtract 40W from both members} \\ \Rightarrow65W-40W=4500 \\ \\ \text{ Simplify the left member} \\ \Rightarrow25W=4500 \\ \\ \text{ Divide both members by 25} \\ \Rightarrow W=(4500)/(25) \\ \\ \text{ Simplify} \\ \Rightarrow W=180 \\ \\ \therefore W=180 \end{gathered}`

Therefore, there were 180 women at first.