Question

Tell if the table shows a linear graph and why

Answer 1

Answer:

The graph is linear

Explanations:

For a graph to be linear, they must have a constant slope at all the segments of the graph

The formula for the slope of a graph is given as:

`\text{Slope = }(y_2-y_1)/(x_2-x_1)`

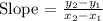
Considering the first two rows of the graph

`\begin{gathered} x_1=-5,x_2=0,y_1=-7,y_2=\text{ -8} \\ \text{Slope = }(-8-(-7))/(0-(-5)) \\ \text{Slope = }(-8+7)/(0+5) \\ \text{Slope = }(-1)/(5) \\ \text{Slope = -0.2} \end{gathered}`

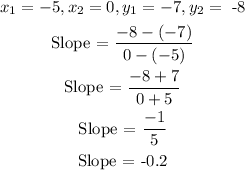
Considering the last two rows of the graph

`\begin{gathered} x_1=5,x_2=10,y_1=-9,y_2=-10 \\ \text{Slope = }(-10-(-9))/(10-5) \\ \text{Slope = }(-10+9)/(5) \\ \text{Slope = }(-1)/(5) \\ \text{Slope = -0.2} \end{gathered}`

Since the slope is constant for all the segments of the graph, the graph is linear.