1 Answer

Bhuwan Gautam · Answer 1 · 2023-11-07T20:03:17+0000

SOLUTION

Write out the expression

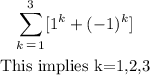
$\begin{gathered} \sum ^3_(k\mathop=1)\lbrack1^k+(-1)^k\rbrack \\ \text{This implies k=1,2,3} \end{gathered}$

Then we substitute k=1 into the expression and obatin the value

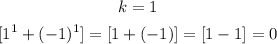
$\begin{gathered} k=1 \\ \lbrack1^1+(-1)^1\rbrack=\lbrack1+(-1)\rbrack=\lbrack1-1\rbrack=0 \end{gathered}$

Similarly,

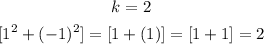
$\begin{gathered} k=2 \\ \lbrack1^2+(-1)^2\rbrack=\lbrack1+(1)\rbrack=\lbrack1+1\rbrack=2 \end{gathered}$

Then we also substitute the last value of k

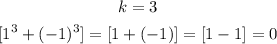
$\begin{gathered} k=3 \\ \lbrack1^3+(-1)^3\rbrack=\lbrack1+(-1)\rbrack=\lbrack1-1\rbrack=0 \end{gathered}$

finally, we take the sum of the result

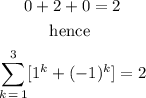
$\begin{gathered} 0+2+0=2 \\ \text{hence } \\ \sum ^3_{k\mathop{=}1}\lbrack1^k+(-1)^k\rbrack=2 \end{gathered}$

Therefore the summation of the expression from 1 to 3 for the values of k is 2

The right option is E (2).

Please log in or register to add a comment.