Question

Find all complex zeros of f (x) = x4 – 10x3 + 35x2 – 46x + 10 given that 3 + i is a zero of f. Then write the linear factorization of f (x).

Answer 1

The given function is

`f(x)=x^4-10x^3-35x^2-46x+10`

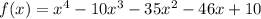
We know that one complex solution is 3 + i, which means the other complex solution is 3-i because complex solutions happen in pairs.

Now, we look for the other two zeros. We can't use synthetic division because the real solutions are not integers. Using a calculator, the solutions are

`\begin{gathered} x\approx0.19 \\ x\approx12.97 \end{gathered}`

Therefore, the linear factorization of f(x) would be

`x^4-10x^3-35x^2-46x+10=(x-0.19)(x-12.97)(x+1.58-1.26i)(x+1.56+1.26i)`