The formula for the exponential decay is as follows.
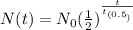
where N(t) is the final value, N₀ is the initial value, t is the time that passed, and t₀.₅ is the half-life.
In given, we have the following.
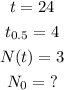
Substituting to the equation, we can solve for N₀.
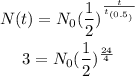
Thus, we have the following.
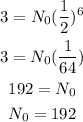
Therefore, the initial mass must be 192 mg.
To solve for the mass in 6 weeks, convert the weeks into days. Note that in 1 week, there are 7 days.
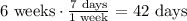
Substitute the given values and the 42 days as t into the equation and then solve for N(t).
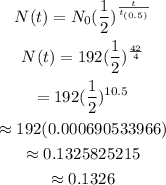
Therefore, in 6 weeks, the mass must be approximately 0.1326 mg.