We are given that a sphere Z moves with a relative speed of 1 m/s with respect to sphere X which moves at 5 m/s. Let's draw the velocity vectors of the spheres:
Where:
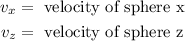
From the relative velocity equation we have:
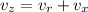
Where:
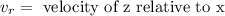
Since we are given the relative velocity we can plug in the values to get the velocity of "z":
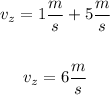
Now, we do the same but now using the sphere Y:
Now, we use the relative velocity equation for these velocities:
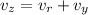
In this case, we have that:
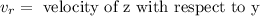
Now, we subtract the velocity of "y" from both sides:
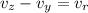
Substituting the values:
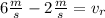
Solving the operations:
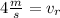
Therefore, the velocity of "Z" relative to "Y" is 4 m/s.