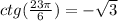Question

Find the exact value for all six trig functions of the angle

Answer 1

We are asked to determine the trigonometric functions for:

`\theta=(23\pi)/(6)`

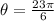
To determine the trigonometric functions we need to determine the equivalent angle that is between 0 and 2pi. To do that we will subtract 2pi from the given angle:

`(23\pi)/(6)-2\pi=(11\pi)/(6)`

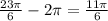
The equivalent angle is 11pi/6. In the unit circle this angle is:

The end-point of this angle is:

`((√(3))/(2),-(1)/(2))`

Since the x-component of the end-point is the cosine, we have:

`cos((23\pi)/(6))=(√(3))/(2)`

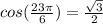
The y-coordinate is the sine, therefore:

`sin((23\pi)/(6))=-(1)/(2)`

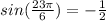
To determine the tangent we use the following relationship:

`tanx=(sinx)/(cosx)`

Substituting we get:

`tan((23\pi)/(6))=(-(1)/(2))/((√(3))/(2))`

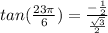
Simplifying we get:

`\begin{gathered} tan((23\pi)/(6))=(-1)/(√(3)) \\ \end{gathered}`

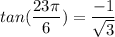
To determine the secant we use the following relationship:

`secx=(1)/(cosx)`

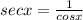
Substituting we get:

`sec((23\pi)/(6))=(1)/((√(3))/(2))`

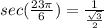
Simplifying we get:

`sec((23\pi)/(6))=(2)/(√(3))`

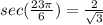
To determine the cosecant we use the following relationship:

`cscx=(1)/(sinx)`

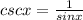
Substituting we get:

`csc((23\pi)/(6))=(1)/(-(1)/(2))`

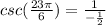
Simplifying we get:

`csc((23\pi)/(6))=-2`

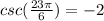
Finally, for the cotangent we use:

`ctgx=(1)/(tanx)`

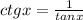
Substituting we get:

`ctgx=(1)/((-1)/(√(3)))`

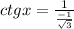
Simplifying:

`ctg((23\pi)/(6))=-√(3)`