The Solution:
Given:
(a) The probability that the next gumball is yellow is:
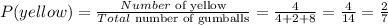
(b) The probability someone gets a
yellow gumball chews it, and then gets a second yellow gumball.
That is, without replacement.
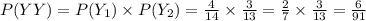
(c) The probability a gumball is orange given that it is not yellow.

Therefore, the correct answers are:
(a) 2/7
(b) 6/91
(c) 4/7