Question

9. Determine whether A=B, A⊆B,B⊆A, A⊂B, B⊂A, or ifnone of these applies.A = {Thursday, Sunday, Tuesday, Wednesday}B = {Thursday, Wednesday}Which of the following are true statements? Select all that apply.❑ A=B❑ A⊆B❑ B⊆A❑ A⊂B❑ B⊂A❑ None of the above statements are true.

Answer 1

To solve this problem, we need to understand three important definitions.

Two sets C and D are said to be equal if and only if all the elements contained on C are also elements of D.

This is represented by the symbol "=" .

Subset: If C and D are sets and every element of C is also an element of D.

C is a subset of D, denoted by "C ⊆ D".

Proper Subset: If C is a subset of D, but C is not equal to D (that is, there exists at least one element of D which is not an element of C), then C is also a proper (or strict) subset of D. this is written as "C ⊂ D".

In our problem, we have two sets A and B. They are

A = {Thursday, Sunday, Tuesday, Wednesday}

B = {Thursday, Wednesday}

As you can see, all the elements contained on B are not all the elements of A, therefore, those groups are not equal and the first option is false.

Every element of B is also an element of A, which means that B is a subset of A.

`B\subseteq A`

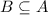
Since B is a subset of A, and they are not equal, B is also a proper subset of A.

`B\subset A`

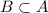
Those are the only true statements.

`\begin{gathered} B\subseteq A \\ B\subset A \end{gathered}`