Step-by-step explanation
From the statement, we have a sample selected from a population with:
• mean μ = 65,
,
• standard deviation σ = 15.
a. The sample has a size n = 9.
• From statistics, we know that the mean value of the sample Mₛ is equal to the mean of the population μ, so we have:
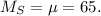
• The standard error of the sample σₛ is given by:
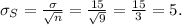
b. The sample has a size n = 25.
• From statistics, we know that the mean value of the sample Mₛ is equal to the mean of the population μ, so we have:
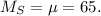
• The standard error of the sample σₛ is given by:
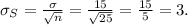
Answer
a.
• Expected mean value = ,65
,
• Expected standard error = ,5
b.
• Expected mean value = ,65
,
• Expected standard error = ,3