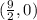Question

What are the coordinates of the point on the directed line segment from (3,3) to (7, -5) that partitions the segment into a ratio of 5 to 3?

Answer 1

Let the coordinates of the point be (x,y).

The following diagram represents the given situation,

Consider that the coordinates of the point that divides the line segment joining two points in ratio m:n, is given by the formula,

`((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))`

According to the given problem,

`\begin{gathered} (x_1,y_1)=(7,-5) \\ (x_2,y_2)=(3,3) \\ m=5 \\ n=3 \end{gathered}`

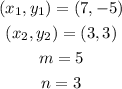
Substitute the values,

`\begin{gathered} =(\frac{5\cdot(3)_{}+3\cdot(7)_{}}{5+3},\frac{5\cdot(3)_{}+3\cdot(-5)}{5+3}) \\ =(\frac{15_{}+21_{}}{8},(15-15)/(8)) \\ =(\frac{36_{}}{8},(0)/(8)) \\ =(\frac{9_{}}{2},0) \end{gathered}`

Thus, the coordinates of the point on the directed line segment from (3,3) to (7, -5) that partitions the segment into a ratio of 5 to 3, is obtained as,

`((9)/(2),0)`