Question

Assume that the iron block is 175 g and that the beaker

contains 75 m hot water, or 75 gince the density of water
is 1.00 if you heat the metal directly on the burner to
about 275°C and then place it in the room temperature (
25° C) water, the temperature of the combined water and
iron equilibrates at 75º C Note that the specific heat of
water is 4.182, J/g•C
Using these values, what is the specific heat of iron in
units of J/g•C? Please answer to the nearest 0.001
J
9 °C

Answer 1

We are given that a hot iron block is placed inside room temperature water. This means that there is a heat transfer from the iron block into the water. The formula for the heat that is transferred is given by:

`q=mc_p\Delta T`

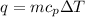
Where "m" is the mass, "cp" is the specific heat and "delta T" is the difference in temperature.

Since the heat leaves the iron and goes into the water, by the principle of conservation of energy, we have the following relationship:

`q_{\text{i}}=-q_{\text{w}}`

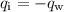
Replacing the formulas for the heat:

`m_{\text{i}}c_(pi)\Delta T_i=-m_wc_(pw)\Delta T_w`

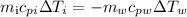
Now we establish the difference in temperature:

`m_ic_(pi)(T_(fi)-T_(0i))=-m_wc_(pw)(T_(fw)-T_(iw))`

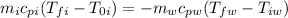
Now we solve for the specific heat of iron:

`c_(pi)=(-m_wc_(pw)(T_(fw)-T_(iw)))/(m_i\mleft(T_(fi)-T_(0i)\mright))`

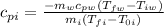
Replacing the values:

`c_(pi)=\frac{-(75g)(4.182(j)/(gC))(75C-25C)}{175g_{}(75C-275)}`

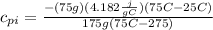
Solving the operations:

`c_(pi)=0.45\text{ J/g\degree{}C}`

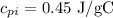
Therefore, the specific heat of iron is 0.45 J/g°C